clifford: Geometric Algebra for Python¶
In [1]: from clifford.g3 import * # import GA for 3D space
In [2]: import math
In [3]: a = e1 + 2*e2 + 3*e3 # vector
In [4]: R = math.e**(math.pi/4*e12) # rotor
In [5]: R*a*~R # rotate the vector
Out[5]: (2.0^e1) - (1.0^e2) + (3.0^e3)
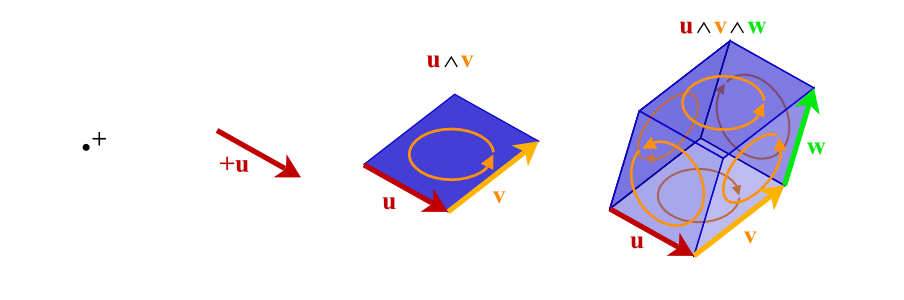
This module implements Geometric Algebras (a.k.a. Clifford algebras). Geometric Algebra (GA) is a universal algebra which subsumes complex algebra, quaternions, linear algebra and several other independent mathematical systems. Scalars, vectors, and higher-grade entities can be mixed freely and consistently in the form of mixed-grade multivectors.