clifford: Geometric Algebra for Python¶
In [1]: from clifford.g3 import * # import GA for 3D space
In [2]: from numpy import e,pi
In [3]: a = e1 + 2*e2 + 3*e3 # vector
In [4]: R = e**(pi/4*e12) # rotor
In [5]: R*a*~R # rotate the vector
Out[5]: (2.0^e1) - (1.0^e2) + (3.0^e3)
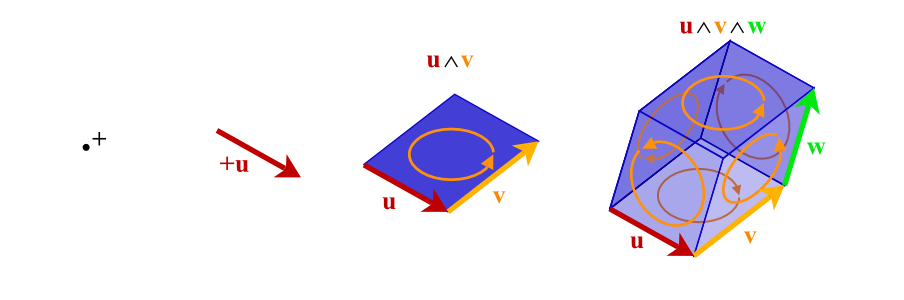
This module implements Geometric Algebras (a.k.a. Clifford algebras). Geometric Algebra (GA) is a universal algebra which subsumes complex algebra, quaternions, linear algebra and several other independent mathematical systems. Scalars, vectors, and higher-grade entities can be mixed freely and consistently in the form of mixed-grade multivectors.
Docs¶
- Tutorials
- Installation
- Quick Start (G2)
- The Algebra Of Space (G3)
- Rotations in Space: Euler Angles, Matrices, and Quaternions
- Conformal Geometric Algebra
- Space Time Algebra
- Interfacing Other Mathematical Systems
- Predefined Geometric Algebras
- Writing high(ish) performance code with Clifford and Numba via Numpy
- Example 1 Interpolating Conformal Objects
- Example 2 Clustering Geometric Objects
Slide Decks¶
Links¶
Symbolic geometric algebra module for python: https://github.com/brombo/galgebra
Cambridge GA group: http://www.mrao.cam.ac.uk/~clifford
David Hestenes’ (The man) website: http://geocalc.clas.asu.edu/
GAOnline - Conformal Geometric Algebra visualiser: http://gaonline.azurewebsites.net/
If you think Geometric Algebra looks interesting and want to learn more, check out the cambridge groups page, and here are some great introductory textbooks!
Geometric Algebra for Physicists, by Doran and Lasenby
Geometric Algebra for Computer Science, by Dorst, Fontijne and Mann
New Foundations for Classical Mechanics, by David Hestenes